問2 次の文章を読み、空欄[ウ]~[カ]に当てはまる数字をマークせよ。
図1に示した部品は、棒状の7個のLEDⓐ~ⓖを使って数字や一部のアルファベットを表示するものである。この部品を7セグメントLEDと呼び、例えば数字の0~9は図2のようにLEDを点灯させて表示することができる。
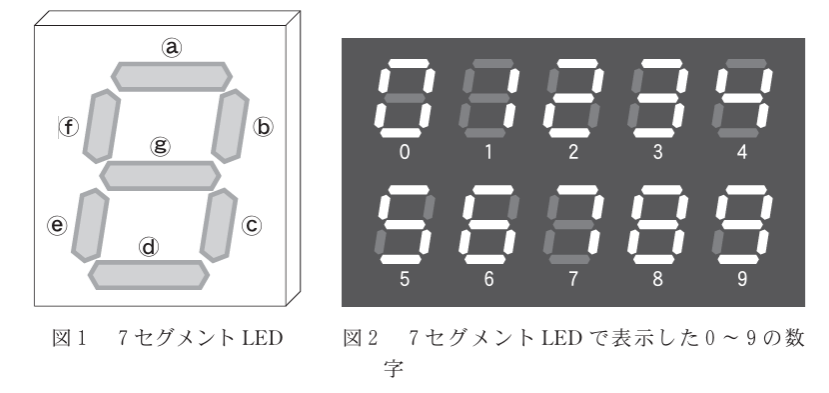
7セグメントLEDにおける、ⓐ~ⓖを点灯させる組み合わせは、すべてのLEDが消灯している状態を含めて全部で[ウ][エ][オ]通りである。
図1に示した部品は、アルファベットとして図3に示す13種類を表示できる。

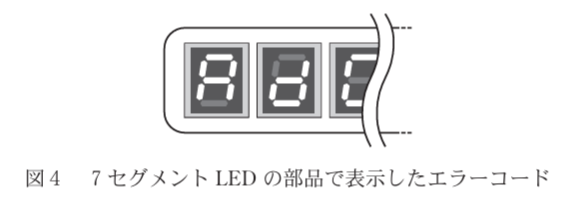
これらの大文字8種類、小文字5種類のアルファベットに加え、数字10種類を用いて、ある製品のエラーコードを表示する。図4のように、1桁目を大文字のアルファベット、2桁目を小文字のアルファベット、3桁目以降の桁については数字のみを用いる場合、図1の7セグメントLEDの部品が全部で少なくとも[カ]個あれば5,000種類のエラーコードを表示することができる。
正解:[ウ]=1, [エ]=2, [オ]=8
この問題は、7個のLED(ⓐ~ⓖ)の点灯パターンの総数を求める問題です。
まず、各LEDの状態を考えます。それぞれのLEDには「点灯する」か「消灯する」かの2通りの状態があります。
- LEDⓐ → 2通り
- LEDⓑ → 2通り
- LEDⓒ → 2通り
- ・・・
- LEDⓖ → 2通り
組み合わせの総数を計算しましょう。
- 7個のLEDが
- それぞれ独立して2通りの状態を持つ
ので、全体の組み合わせの数は、それぞれの通り数をすべて掛け合わせることで求められます。
計算式は次のようになります。
2×2×2×2×2×2×2×2=2⁷ = 128
したがって、すべてのLEDが消えている状態を含め、全部で 128 通りの組み合わせがあります。
正解:[カ]=5
この問題は、指定されたルールで5,000種類以上のエラーコードを表示するために、最低何桁の7セグメントLEDが必要かを求める問題です。
まず、エラーコードのルールを確認しましょう。
- 1桁目
大文字アルファベット → 8種類 (A, E, F, H, J, L, P, U) - 2桁目
小文字アルファベット → 5種類 (b, c, d, n, y) - 3桁目以降
数字 → 10種類 (0〜9)
桁数ごとに何通りのコードが作れるか計算します。
エラーコードの総桁数をnとします。 作れるコードの総数は、以下の式で計算できます。
(1桁目の種類)×(2桁目の種類)×(3桁目以降の種類の数)
8×5×10⁽ⁿ⁻²⁾
この総数が 5,000以上 になる最小のnを探します。
8×5×10⁽ⁿ⁻²⁾>=5000
を計算すると、少なくとも 5桁 あれば5,000種類のエラーコードを表示できるとわかります。
この記事で掲載・解説している問題の著作権は、独立行政法人大学入試センターに帰属します。


コメント