問1 次の問い(a・b)に答えよ。
a 次の文章中の空欄[ア]に入れるのに最も適切なものを、後の⓪~④のうちから一つ選べ。
インターネットで情報をやり取りする際、発信者が本人であることを確認するためにデジタル署名が利用できる。また、デジタル署名を用いると、その情報が[ア]を確認できる。
⓪複製されていないか
①暗号化されているか
②改ざんされていないか
③どのような経路で届いたか
④盗聴されていないか
正解:②改ざんされていないか
この問題は「デジタル署名」の役割について尋ねています。
デジタル署名には、主に2つの大きな役割があります。
- 本人証明(誰が送ったか)
文章にある通り、情報の発信者が「本人であること」を確認できます。これは、本人の「秘密鍵」でしか作れない署名を「公開鍵」で検証することで実現します。 - 完全性の保証(中身が変わっていないか)
送られた情報が、途中で誰かに書き換えられていないこと(改ざんされていないこと)を確認できます。
今回の問題文では、前半で1つ目の役割である「本人証明」についてすでに説明されています。
そのため、空欄[ア]には2つ目の重要な役割である「改ざんされていないか」が入るのが最も適切です。
⓪複製されていないか
デジタルデータは簡単に複製(コピー)できるのが特徴です。デジタル署名は、複製を防ぐ技術ではありません。
①暗号化されているか
「暗号化」は、情報を第三者に読み取られないように隠す(秘密にする)ための技術です。デジタル署名は本人証明と改ざん検知が目的であり、情報そのものを隠すわけではありません。(しばしば暗号化とセットで使われますが、役割は別です。)
③どのような経路で届いたか
情報がどのサーバーやルーターを通ってきたかという通信経路を知るためのものではありません。
④盗聴されていないか
「盗聴」を防ぐのは「暗号化」の役割です。デジタル署名だけでは、通信の途中で情報を盗み見られることを防げません。
b 近年、128ビットで構成されるIPアドレスが利用されるようになった理由の一つとして最も適当なものを、次の⓪~④のうちから一つ選べ。
[イ]
⓪有線LANだけでなく無線LANにも対応するため。
①大容量データの送受信に対応するため。
②インターネットに直接接続する機器の増加に対応するため。
③漢字などの英数字以外の文字で表されるドメイン名に対応するため。
④HTMLの仕様変更に対応するため。
正解:②インターネットに直接接続する機器の増加に対応するため。
この問題は、なぜ新しいIPアドレスの仕組みが必要になったかを尋ねています。
ポイントは「IPアドレスの枯渇(こかつ)」です。
昔のIPアドレス (IPv4)は32ビットで構成されています。つまり、約43億個 (2の32乗)のアドレスしか作れません。インターネットが始まった当初はこれで十分だと考えられていました。
しかし、今はパソコンやスマートフォンだけでなく、家電、車、センサーなど、あらゆるモノがインターネットに接続されるようになりました(IoT)。その結果、世界中の機器にIPアドレスを割り当てると、約43億個ではまったく足りなくなってしまいました。これが「IPアドレスの枯渇問題」です。
この問題を解決するために、128ビットで構成される新しいIPアドレス (IPv6) が作られました。約340澗(かん)個(2の128乗)という、ほぼ無限に近い数のアドレスが利用できるようになりました。
これにより、今後どれだけインターネットに接続する機器が増えても対応できるようになったのです。
したがって、128ビットのIPアドレスが利用されるようになった最大の理由は「インターネットに直接接続する機器の増加に対応するため」となります。
⓪有線LANだけでなく無線LANにも対応するため。
古いIPv4でも、問題なく無線LANは利用できます。これは理由になりません。
①大容量データの送受信に対応するため。
データの容量とIPアドレスのビット数は直接関係ありません。通信速度などは別の技術で決まります。
③漢字などの英数字以外の文字で表されるドメイン名に対応するため。
漢字などのドメイン名は「国際化ドメイン名(IDN)」という別の仕組みで実現されています。IPアドレスの仕組みとは直接関係ありません。
④HTMLの仕様変更に対応するため。
HTMLはウェブページを作るための言語です。IPアドレスは通信の宛先を示すもので、全く違う技術なので関係ありません。
問2 次の文章を読み、空欄[ウ]~[カ]に当てはまる数字をマークせよ。
図1に示した部品は、棒状の7個のLEDⓐ~ⓖを使って数字や一部のアルファベットを表示するものである。この部品を7セグメントLEDと呼び、例えば数字の0~9は図2のようにLEDを点灯させて表示することができる。
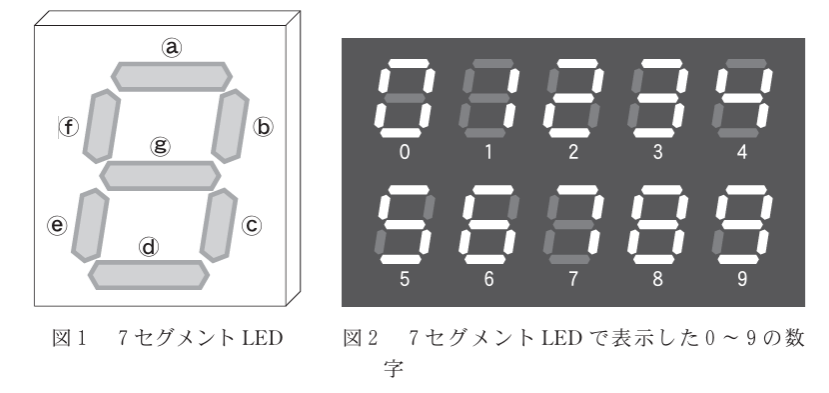
7セグメントLEDにおける、ⓐ~ⓖを点灯させる組み合わせは、すべてのLEDが消灯している状態を含めて全部で[ウ][エ][オ]通りである。
図1に示した部品は、アルファベットとして図3に示す13種類を表示できる。

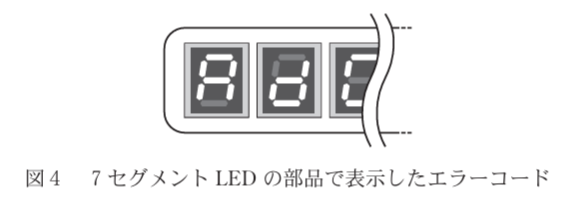
これらの大文字8種類、小文字5種類のアルファベットに加え、数字10種類を用いて、ある製品のエラーコードを表示する。図4のように、1桁目を大文字のアルファベット、2桁目を小文字のアルファベット、3桁目以降の桁については数字のみを用いる場合、図1の7セグメントLEDの部品が全部で少なくとも[カ]個あれば5,000種類のエラーコードを表示することができる。
正解:[ウ]=1, [エ]=2, [オ]=8
この問題は、7個のLED(ⓐ~ⓖ)の点灯パターンの総数を求める問題です。
まず、各LEDの状態を考えます。それぞれのLEDには「点灯する」か「消灯する」かの2通りの状態があります。
- LEDⓐ → 2通り
- LEDⓑ → 2通り
- LEDⓒ → 2通り
- ・・・
- LEDⓖ → 2通り
組み合わせの総数を計算しましょう。
- 7個のLEDが
- それぞれ独立して2通りの状態を持つ
ので、全体の組み合わせの数は、それぞれの通り数をすべて掛け合わせることで求められます。
計算式は次のようになります。
2×2×2×2×2×2×2×2=2⁷ = 128
したがって、すべてのLEDが消えている状態を含め、全部で 128 通りの組み合わせがあります。
正解:[カ]=5
この問題は、指定されたルールで5,000種類以上のエラーコードを表示するために、最低何桁の7セグメントLEDが必要かを求める問題です。
まず、エラーコードのルールを確認しましょう。
- 1桁目
大文字アルファベット → 8種類 (A, E, F, H, J, L, P, U) - 2桁目
小文字アルファベット → 5種類 (b, c, d, n, y) - 3桁目以降
数字 → 10種類 (0〜9)
桁数ごとに何通りのコードが作れるか計算します。
エラーコードの総桁数をnとします。 作れるコードの総数は、以下の式で計算できます。
(1桁目の種類)×(2桁目の種類)×(3桁目以降の種類の数)
8×5×10⁽ⁿ⁻²⁾
この総数が 5,000以上 になる最小のnを探します。
8×5×10⁽ⁿ⁻²⁾>=5000
を計算すると、少なくとも 5桁 あれば5,000種類のエラーコードを表示できるとわかります。
問3 次の文章を読み、空欄[キ]に当てはまる数字をマークせよ。また、空欄[ク]に入れるのに最も適当なものを、後の解答群のうちから一つ選べ。
チェックディジットは、書籍のISBNコードなどで数字の入力ミスを検出するためなどに利用されている。ここでは、5桁の数字(N₅N₄N₃N₂N₁)の利用者IDに、チェックディジット1桁(C)を加えた6桁の識別番号(N₅N₄N₃N₂N₁C)を考える。チェックディジットの生成方法として、次の2種類を考える。
【生成方法A】利用者IDの各桁の値を足し合わせ、10で割ったあまりRを求め、10からRを引いた値をチェックディジットとする。
【生成方法B】利用者IDの各奇数桁(N₅, N₃, N₁)の値尾をそれぞれ3倍にした値と、各偶数桁(N₄, N₂)の値を足し合わせ、10で割ったあまりRを求め、10からRを引いた値をチェックディジットとする。
なお、いずれの生成方法も、Rが0の場合は、チェックディジットを0とする。
例えば,ある利用者IDが「22609」の場合にチェックディジットを計算すると、生成方法Aでは「1」になり、生成方法Bでは[キ]となる。
これらのチェックディジットでは、1桁の入力ミスは検出できても、2桁の入力ミスは、検出できないことがある。生成方法Bはこの点について多少検出できるように工夫されている。例えば、[ク]入力ミスをした場合は、生成方法Aでは検出できることはないが、生成方法Bでは検出できることがある。
[ク]の解答群
⓪奇数桁の数字を二つ間違える
①連続する二つの桁の数字をそれぞれ間違える
②奇数桁のうちの二つの桁の数字の順序を逆にする
③連続する二つの桁の数字の順序を逆にする
正解:7
これは、利用者ID「22609」に対して【生成方法B】を使ってチェックディジットを計算する問題です。
①奇数桁(N₅, N₃, N₁)の値をそれぞれ3倍して足し合わせましょう。
- N₅ = 2 → 2×3= 6
- N₃ = 6 → 6×3= 18
- N₁ = 9 → 9×3= 27
合計:6 + 18 + 27 = 51
②偶数桁(N₄, N₂)の値を足し合わせます。
- N₄ = 2
- N₂ = 0
合計:2 + 0 = 2
③それぞれ求めた合計を足し合わせます。
51 + 2 = 53
④合計を10で割った余りRを求めます。
53 ÷ 10 = 5あまり3
R = 3
⑤0からRを引いた値をチェックディジットとします。
10 – 3 = 7
したがって、[キ]に入る数字は7です。
正解:③連続する二つの桁の数字の順序を逆にする
これは、「生成方法Aでは検出できないが、生成方法Bでは検出できることがある」2桁の入力ミスはどれか、という問題です。
この種のエラーで最も代表的なのが「隣接する2つの数字の入れ替わり(転置誤差)」です。
生成方法A(単純な和)の場合
隣り合う数字aとbを入れ替えても、合計は a + b から b + a になるだけで、和は変わりません。そのため、この方法では隣接する数字の入れ替わりは絶対に検出できません。
生成方法B(重み付きの和)の場合
例えば、奇数桁のaと偶数桁のbを入れ替えたとします。
元の計算(一部):3 × a + 1 × b
間違った計算(一部):3 × b + 1 × a
この差は
(3b + a) – (3a + b)
= 2b – 2a
= 2(b – a)
となります。
この差が10の倍数にならない限り、エラーとして検出できます。(例えば、aとbの差が5の場合など)
この条件に最も合致するのは、選択肢③「連続する二つの桁の数字の順序を逆にする」です。
⓪奇数桁の数字を二つ間違える
もし、この間違いが原因で生成方法Aが検出に失敗するケースを考えてみましょう。
それは、間違いによる数字の変化の合計が10の倍数になった場合です。(例:一方の数字が2増え、もう一方が2減るなど)
生成方法Aでの変化:(a´- a) + (b´- b) = 10 × k(kは整数)
この場合、合計の変化がないので検出できません。
生成方法Bでの変化:奇数桁はどちらも3倍されるので、変化は3(a´- a) + 3(b´- b) となります。これは、((a´- a) + (b´- b)) となり、3 × (10 – k) となります。
この値も必ず10の倍数になってしまいます。
つまり、このタイプの間違いを生成方法Aが見逃す場合、生成方法Bも必ず見逃してしまいます。したがって、条件に合いません。
①連続する二つの桁の数字をそれぞれ間違える
これは間違いとは言えませんが、③よりも不適切です。 この選択肢は非常に範囲が広いです。「数字を間違える」というだけでは、どんな間違い方なのかが特定できません。
例えば、「12」を「31」と間違えたとします。
元の数字の和:1 + 2 = 3
間違った数字の和:3 + 1 = 4
この場合、和が変わるので生成方法Aでも検出できてしまいます。
この選択肢には、正解である③「順序を逆にする」という特殊なケースが含まれています。問題では「最も適当なもの」を選ぶ必要があるため、このエラーの典型例であり、生成方法Aが絶対に検出できないパターンを具体的に示している③の方が、より優れた解答となります。
②奇数桁のうちの二つの桁の数字の順序を逆にする
これは不適切です。 例えば、N₅とN₃の数字を入れ替えたとします。
生成方法A:足し算なので、数字の順番が変わっても合計は変わりません。よって、検出できません。
生成方法B:奇数桁の数字は、どちらも同じように3倍されます。そのため、入れ替えても計算結果は変わりません。
両方の方法で検出できないため、条件に合いません。
問4 次の文章を読み、後の問い(a・b)に答えよ。
マウスカーソルをメニューやアイコンなどの対象物に移動する操作をモデル化し、Webサイトやアプリケーションのユーザインタフェースをデザインする際に利用されている法則がある。この法則では、次のことが知られている。
- 対象物が大きいほど、対象物に移動するときの時間が短くなる。
- 対象物への距離が短いほど、対象物に移動するときの時間が短くなる。
a 次の文章中の空欄[ケ]に入れるのに最も適当なものを、図の⓪~③のうちから一つ選べ。
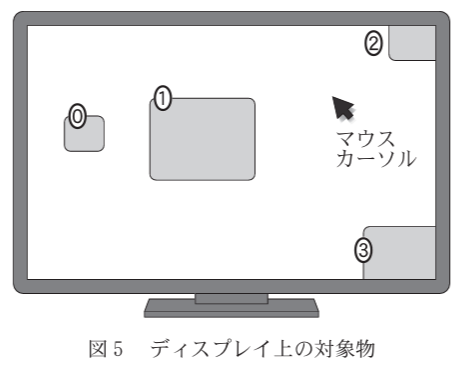
この法則では、PCなどでマウスを操作する場合、マウスカーソルはディスプレイの端で止まるため、ディスプレイの端にある対象物は実質的に大きさが無限大になると考える。
この法則に基づくと、図の⓪~③で示した対象物のうち、現在ディスプレイ上の黒矢印で示されているマウスカーソルの位置から、最も短い時間で指し示すことができるのは[ケ]である。
正解:②
この問題は、UIデザインで有名な「フィッツの法則」に基づいています。この法則のポイントは2つです。
- 対象物が大きいほど、速く指し示せる
- カーソルからの距離が近いほど、速く指し示せる
これに加えて、問題文にはPC操作における重要なヒントが書かれています。
「ディスプレイの端にある対象物は、実質的に大きさが無限大になる。」
これは、マウスカーソルが画面の端で止まるため、勢いよくマウスを端まで動かせば、細かい照準を合わせる必要がないからです。特に画面の四隅は、上下と左右の二方向に対して大きさが無限大とみなせるため、最も簡単にポイントできる場所となります。
⓪
この選択肢は、距離と大きさの両方の面で不利です。
①よりも遠く、②や③のような画面の端にあるというアドバンテージもありません。明らかに最も時間がかかる選択肢と言えます。
①
距離が近い点は有利ですが、このオブジェクトは画面の内部にあり、大きさが有限です。
つまり、ターゲットを通り過ぎないように、カーソルを正確に動かして止める「減速」と「照準合わせ」の操作が必要です。この微調整に時間がかかってしまいます。
③
大きさが無限な点では有利ですが、このオブジェクトは現在のカーソルの位置から②よりも遠い位置にあります。
b 次の文章中の空欄[コ]・[サ]に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。
操作時間を短くするためにこの法則を適用した事例として、利用頻度に基づいてメニュー項目を配置する方法がある。
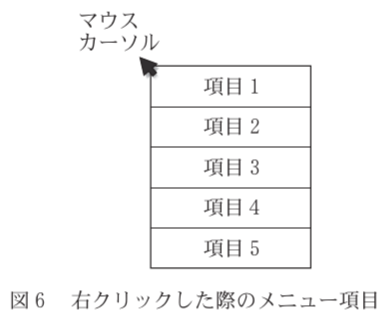
ここでは、マウスを右クリックした際に、マウスカーソルに対して図に示すような位置で表示されるメニュー項目の配置について考える。マウスカーソルで選択できる各メニュー項目の大きさは同じであるとし、この法則のみに沿って設計されたとすると、「項目」は、他の項目と比べ利用頻度が[コ]項目なので、意図的に[サ]に配置されていると考えられる。
[コ]の解答群
⓪低い
①同程度の
②高い
[サ]の解答群
⓪メニューの中で一番目立つ場所
①マウスカーソルの位置から遠い場所
②マウスで素早く選択できる場所
正解:
[コ]=⓪低い,
[サ]=①マウスカーソルの位置から遠い場所
この問題は、前の問題に引き続き「フィッツの法則」を応用したものです。この法則の要点は「カーソルから近い対象物ほど、速く選択できる」という点です。
【コ】の考え方
まず、メニューの設計原則を理解しましょう。このメニューは「利用頻度」に基づいて、操作時間が短くなるように設計されています。つまり、よく使う項目ほど、速く選択できる場所に配置されるはずです。
図6を見ると、「項目5」はマウスカーソルから最も遠い位置にあります。フィッツの法則によれば、最も遠い位置は、選択するのに最も時間がかかる(=遅い)場所です。
最も遅い場所に配置されているということは、その項目はあまり使われない、つまり利用頻度が「低い」と判断するのが合理的です。
①同程度の
もし他の項目と利用頻度が同じくらいなのであれば、わざわざ一番遠くて操作しにくい(=時間がかかる)場所に配置する積極的な理由がありません。
メニュー設計では、特に優先順位がない限り、関連する項目をまとめたり、アルファベット順にしたりするのが一般的です。「意図的に」遠くに置いた、と考えるには根拠が弱くなります。
②高い
これは正解とは全く逆の考え方です。もし「項目5」の利用頻度が高いのであれば、フィッツの法則に従って、マウスカーソルから最も近い場所(=最も速く選択できる場所)、つまり「項目1」のような位置に配置されるはずです。
利用頻度の高い項目を、わざわざ最も不便な場所に置くのは、操作時間を短くするという設計目的と矛盾します。
【サ】の考え方
【コ】の結論から続けます。「項目5」は利用頻度が低いため、意図的に操作しにくい(=時間がかかる)場所に配置されています。
では、「操作に時間がかかる場所」とは具体的にどこでしょうか。
フィッツの法則に照らし合わせると、それは「マウスカーソルの位置から遠い場所」です。
したがって、利用頻度が低い「項目5」は、意図的に①マウスカーソルの位置から遠い場所に配置されていると考えられます。
⓪メニューの中で一番目立つ場所
「目立つ」というのは、色や太字、アイコンの有無といった視覚的なデザインの話です。
一方で、この問題で問われているフィッツの法則は、カーソルを動かす物理的な時間と距離に関する法則です。
一番遠い場所が必ずしも一番目立つとは限りませんし、操作の速さとは直接関係がありません。論点がずれています。
②マウスで素早く選択できる場所
これも正解とは全く逆の選択肢です。「素早く選択できる場所」とは、フィッツの法則によれば「マウスカーソルの位置から近い場所」を指します。
これは利用頻度の高い項目を置くための場所です。利用頻度が低い「項目5」は、その正反対の場所に配置されているため、この説明は当てはまりません。
この記事で掲載・解説している問題の著作権は、独立行政法人大学入試センターに帰属します。


コメント